データを加工して圧縮率を高めよう:コーディングに役立つ! アルゴリズムの基本(9)(1/5 ページ)
プログラマたるものアルゴリズムとデータ構造は知っていて当然の知識です。しかし、教科書的な知識しか知らなくて、実践的なプログラミングに役立てることができるでしょうか(編集部)
圧縮率を上げるために、ひと工夫
前回「データ量を操る圧縮/展開を究めよう」では、圧縮アルゴリズムの基本としてランレングス法とハフマン符号を紹介しました。今回は、データを圧縮しやすいように加工することで、より圧縮率を上げるアルゴリズムを紹介していきたいと思います。
さて、圧縮率を上げるにはどうすればよいでしょうか。
ランレングス法では、連続する文字列が多ければ多いほど圧縮率が高まります。ハフマン符号では、できるだけ特定の文字が多く出現するようになっていれば圧縮率が高まります。このようなデータの加工の手法を見ていきます。
ブロックソーティング
まず、連続する文字列を多くするアルゴリズムを紹介します。ブロックソーティングと呼ばれる手法です。
ブロックソーティングは、Burrows-Wheeler変換とも呼ばれます。この手法は、マイケル・バロウズ(Michael Burrows)とデビッド・ホイーラー(David Wheeler)が考案しました。bzip2の圧縮にも使われているアルゴリズムです。
ブロックソーティングそのものはデータを圧縮するものではありません。データを並べ替えて連続するデータを増やし、圧縮しやすくするものです。
ブロックソーティングによる変換
早速、ブロックソーティングとはどのようなものなのかを見ていきましょう。まず、変換の方法を紹介します。
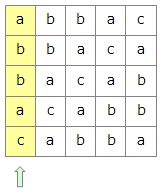
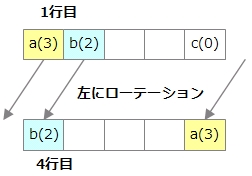
「abbac」という文字列があったとします。この文字列を、1文字左にローテーションすると、「bbaca」という文字列になります。さらに1文字ローテーションすると、「bacab」という文字列になります。
この要領で文字数分ローテーションさせます。1文字ずつローテーションした文字列を縦に並べると5×5の正方形のブロックになります。
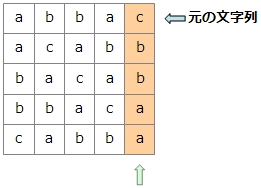
このブロックを、一番左の列を基準にソートします。一番左の列の文字がすべて同じ場合は、左から2番目の列の文字を対象にします。左から2番目の列の文字も同じだった場合は、3番目、4番目と見ていきます。
ソートした結果から、一番右の列の文字を上から取り出せば変換終了です。この例では「cbbaa」となります。また、元の文字列が何行目に出てきたかを記録しておきます。この例では1行目です。
こうしてできたデータが、連続した文字が多くなるのはなぜでしょうか。英語の文章の場合、「the」などの頻繁に出てくる単語があります。ローテーションしてできた文字列の先頭が「he」の場合、末尾は「t」になっているケースが多くなるはずです。そうすると変換後の文字列では「t」が連続したものになる、ということです。
ブロックソーティングによる復元
ここで、「連続した文字を多くするだけならば、わざわざブロックにしなくても文字をソートするだけでよいではないか」と思われた方もいるかもしれません。なかなか鋭い指摘です。
しかし、単純にソートしてしまうと元の文字列に戻すことができなくなります。ブロックソーティングでは変換後の文字列から元の文字列に復元することができます。ここがブロックソーティングのアルゴリズムの素晴らしいところです。
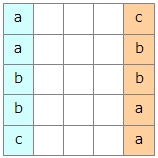
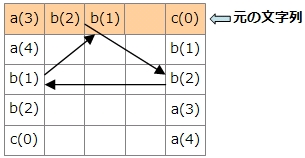
では、復元の手順を見ていきましょう。変換後の文字列を、文字の順にソートします。こうするとブロックの一番左側の列が得られます。
このとき注意しなければならないのは、このソートを安定ソートにしなければならないということです。安定ソートというのは、同じ文字だった場合に、元の順序を保つようにソートすることです。
例えば、「bba」という文字列をソートすると「abb」になります。同じ「b」の文字でも、左側にあった「b」と右側にあった「b」は別物として考えてください。この「bb」の部分で、もともと左にあったbが左に来て、右にあったbが右に来るようなソートが安定ソートです。
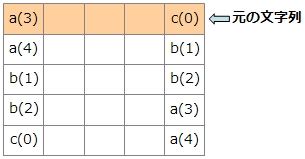
一番右の列に上から番号を付けると分かりやすくなります。a(3)、a(4)と、b(1)、b(2)の部分で順序が保たれています。
次に、元の文字列があった行が何行目か記録してありましたので、その行に着目します。この例では1行目でした。
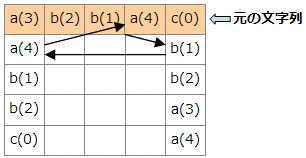
1行目の左の文字はa(3)です。a(3)の右の文字は何になるでしょうか。一番右の列でa(3)が出てくる4行目に注目します。4行目の一番左の文字はb(2)です。もともと左にローテーションしてこういう形になっているので、a(3)の左はb(2)のはずです。
同様に、b(2)の右の文字を調べるには、b(2)が右端にある行を見て、その一番左の文字を調べます。同じ手順で元の文字列「abbac」を復元できました。
Copyright © ITmedia, Inc. All Rights Reserved.