[AI・機械学習の数学]総和を表すΣは機械学習に必須の記号:AI・機械学習の数学入門(5/5 ページ)
応用:重心を求める
もう少し応用的なお話もしておきましょう。機械学習の一つにクラスタリングと呼ばれる方法があります。これは、データを幾つかのグループに分けるのに使われる手法です。そのときに、各グループのデータの「重心」を求める必要があり、そのためにも平均値が使われます。
重心とは、各データからの距離の二乗和が最小になる点のことなので、やはり平均値に他なりません。小学校の頃から慣れ親しんできた平均値がここでも大活躍です。
平面上の二点の距離を求める方法については、この連載の第1回で見ました。そのときには具体的な数値を使って計算しましたが、文字式を使って表してみましょう。
は、図4の斜辺の長さに当たります。
ピタゴラスの定理を使って計算すると、
は、
ですね。いちいち√を求めるのも面倒なので、2乗のままにしておきましょう。つまり、
は、
ということになります。
次に、複数の点の重心を求めてみましょう。重心の座標を
とします。
が
を求めればいいですね。
上の図では、点は4つしか描かれていませんが、点が(x1,y1),(x2,y2)...(xn,yn)のようにたくさんあるなら、
は、
となりますね。これをΣを使って表せば、
となります。この式の値を最小にする
の値は、それぞれの平均値なので、
です。これが重心の座標です*2。
軸(変数)がもう一つ増えて、三次元になっても同様に計算できます(図6)。考え方は同じですが、ちょっと複雑に見えるので、動画での解説も用意してあります(動画3)。
動画3 重心の座標を求める(三次元編)
求めたい距離は、
で、図6のCの長さに当たります。ここでは、三角形ABCが直角三角形になっていることに注目してください。直角三角形ということは、やはりピタゴラスの定理が使えますね。つまり、
です。
A2は上で求めた通り、
です。B2は
です。よって、C2は、
であることが分かります。
Copyright© Digital Advantage Corp. All Rights Reserved.
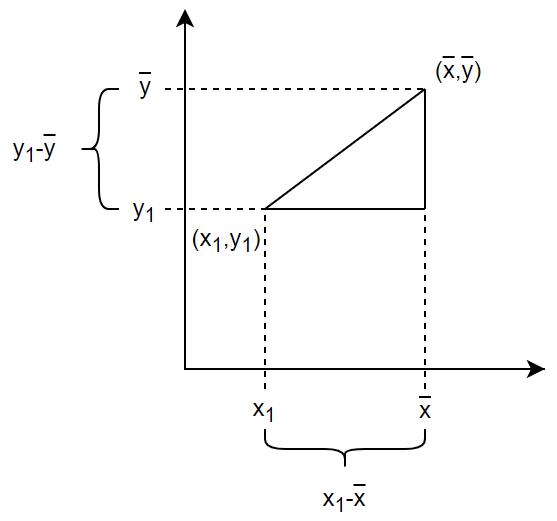 図4 2点の距離
図4 2点の距離
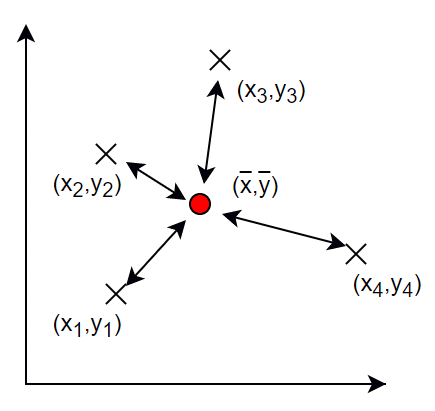 図5 重心
図5 重心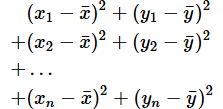
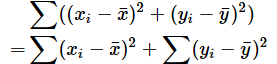
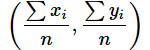

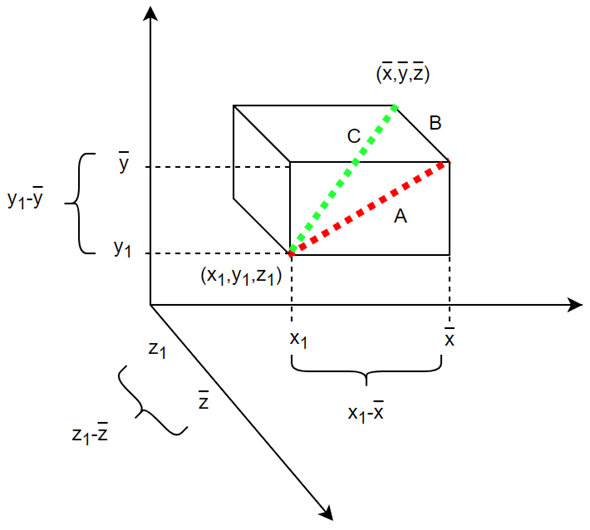 図6 2点の距離(三次元)
図6 2点の距離(三次元)


