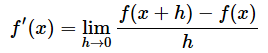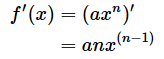[AI・機械学習の数学]微分法の基本を身につけて「変化」を見極めよう:AI・機械学習の数学入門(3/3 ページ)
練習問題
以下の関数を微分してみましょう。
(1) f(x) = 7x3をxで微分する
(2) f(x) = 10をxで微分する
(3) f(x) = 2x4+3x2+5をxで微分する
(4) f(t) = t2−4t+4をtで微分する
解答
(1) f'(x) = 21x2
(2) f'(x) = 0
(3) f'(x) = 8x3 + 6x
(4) f'(t) = 2t−4
(1)は、指数が3なのでそれを係数に掛けて、7 × 3=21が導関数の係数になりますね。指数の方は1つ減らすと2です。よって、21x2となります。
(2)は、ちょっとひっかけっぽいですが、定数項しかないので、0になります。f(x)の値は常に10なので、全く変化しませんね。だから変化率は0です。
(3)は、手順通り各項を計算していけば求められます。
(4)は変数としてtを使っただけです。やはり手順は同じです。
解説(続き):微分の定義と計算方法について
微分の意味や定義も分かった、計算方法も分かった、めでたしめでたし……と言いたいところですが、「いや、ちょっと待ってくれ」と思った人はいないでしょうか。微分の定義は以下のようなものでした。
そして、計算方法は以下のようなものでした。
のとき、
これでは、定義と計算方法がどうつながっているのかが分かりませんね。意味もやり方も分かったから、なんだか分からない面倒な途中の話はいいや、と投げ出さずに、上の定義と下の計算方法がつながっている(=導き出せる)ことを確認してみましょう。ただし、厳密に証明するとかなり長くなるので、簡単な例で答えが合っていることだけを確かめるにとどめます。
では、例として、f(x)=ax2を取りあげます。この導関数を微分の定義に当てはめて計算してみましょう。簡単な例とはいえ、式の変形が少し細かくなるので動画も用意しておきました。
動画3 導関数を求める(二次関数の例)
Copyright© Digital Advantage Corp. All Rights Reserved.