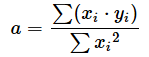［AI・機械学習の数学］微分法を応用して、回帰分析の基本を理解する：AI・機械学習の数学入門（2/2 ページ）

目標【その3】： 最小二乗法による回帰分析の超簡単な例

　既にお話ししたように、回帰分析では各データの最も近くを通る回帰式の定数項と係数を求めます。そのためには「各データと回帰式のy方向の距離（誤差）の二乗の総和」を求め、それが最小になるように定数項と係数を決めればいいということでした（このような方法のことを「最小二乗法」と呼びます）。ここからは、実際にそういった計算をしていきます。

　とはいえ、最初なのでできるだけ簡単な例にしましょう。目標その1で見た面積と家賃の例を使うことにします。面積が0なら家賃も0だと考えていいでしょうから、定数項は0とします。つまり、この単回帰分析の回帰式は、前のページで解説したy＝b＋axに当てはめると以下のようになります。

　yが家賃、xが面積、aは係数です（bは0なので消えます）。簡単すぎますね。でも、最初から複雑な例に取り組もうとしても訳が分からなくなるだけなので、あえてここからスタートします。

　答えを先に示しておきましょう。求めたい値は、各データを(x₁,y₁),(x₂,y₂), ... ,(x_n,y_n)で表したときに、各データと回帰式との間の誤差の二乗和が最小になるときのaの値です。aを求める式は最終的に、

となります。うひゃあ、簡単な例でもこんなに難しいの？　と驚いた人もいるかもしれませんが、日本語で読み下せば恐るるに足らずです。

　分子は「各データのxとyを掛けたものの総和」ですね。それを、分母の「xの二乗和」で割った値、ということになります。
　具体例を当てはめると、分子は「各データの面積×家賃を総合計したもの」で、分母は「各データの面積の二乗を総合計したもの」です。

　というわけで、式の計算内容（どういう計算なのか）は分かったと思います。謎なのは、どうやってこの式が導き出されるのかということですね。

　今回の目標は、この式の計算内容が理解できること（もうできましたね）と、ちゃんと導き出せることです。一歩ずつ確実に進めていけば、必ずこの式にたどり着けるのでご心配なく。一緒に見ていきましょう。

解説：最小二乗法による回帰分析の超簡単な例（具体的な例）

　いきなり、Σ満載の式をお見せしましたが、実感が湧くように、具体例を使って答えを導き出す流れを見ておきましょう（ここからの説明には動画も用意してあります）。

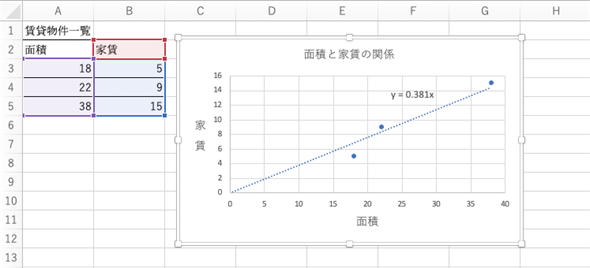
　まず、図7（図1の再掲）の表から面積と家賃の最初（＝表中の3行目）のデータを見てください。

図7　面積と家賃のデータとグラフ（図1の再掲）

　最初のデータは面積xが18、家賃yが5です。もし、家賃が（前述のように）y＝axで求められるなら、直線上の点のy座標は18aです。