PyTorchでCIFAR-10を処理するオートエンコーダーを作ってみよう:作って試そう! ディープラーニング工作室(2/2 ページ)
学習とその結果
ここでは幾つかの設定を変更しながら、3種類の方法でCIFAR-10の画像データをエンコード/デコードするオートエンコーダーを学習させてみます。
- 上で作成した3072次元のデータを128次元に圧縮するニューラルネットワークモデル(エポック数100)
- 3072次元のデータを384次元に圧縮するニューラルネットワークモデル(エポック数100)
- 2番目のニューラルネットワークをさらに200エポック学習させる(エポック数は計300)
一番上の設定は圧縮後の次元数が128です。前回は圧縮後の次元数が2だったので、今回はもっとちゃんとした画像を復元できそうなことが期待できます。これを確認するのが最初のニューラルネットワークモデルといえるでしょう。
さらに、最初とその次のニューラルネットワークモデルでは、圧縮後の次元数に差があります(エポック数は同じ)。そこで、圧縮後の次元数が復元後のデータにどんな影響を与えるかが想像できます(実際には実験は回数を重ねることが重要ですから、たった一度の実験では確たることはいえないことには注意が必要です)。「次元数が多い方が結果もよくなりそう」というのが筆者の期待ですが、そのようになるかを確認することが目的です。
2つ目と3つ目では、同じニューラルネットワークモデルでも100エポックの学習をしたものと、300エポックの学習をしたものとで差が出るかを確認します。ここでも「学習を(ある程度)進めたものの方がよい結果が出る」ことが期待されます。
圧縮後128次元、エポック数100のニューラルネットワークモデルの学習
というわけで、1つ目のニューラルネットワークモデル(とは、上で作成したencoderオブジェクトとdecoderオブジェクトを受け取ったAutoEncoder2クラスのインスタンスです)を使って学習をしてみましょう。
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(net.parameters(), lr=0.5)
EPOCHS = 100
output_and_label, losses = train(
net, criterion, optimizer, EPOCHS, trainloader, input_size)
このコードの実行が終わるまでに、Google Colab環境でおおよそ1時間半弱が必要でした(CPUのみを使用。以下同様)。今回のコードのノートブックで安易に実行ボタンをクリックしないようにしましょう。なお、このコードはエポックごとの平均損失を表示するだけなので、ここでは実行結果の表示は省略します。
これもまた前回同様のコードですが、以下を実行して、どんな画像が復元されたかを確認してみましょう。
img, org = output_and_label[-1]
img = img.reshape(-1, 3, 32, 32)
org = org.reshape(-1, 3, 32, 32)
imshow(org)
imshow(img)
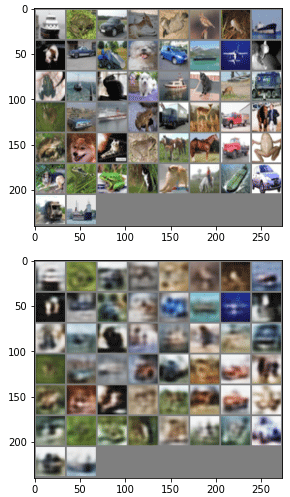
変数output_and_labelの最後の要素は、最後に行った学習での出力とそれに使用した元画像が含まれています。このコードはそれらを取り出して、画像として表示しています。実際の結果を以下に示します。
前回よりはかなりまともな結果になっています。が、全体に「ぼや〜ん」とした結果が得られました。1時間半待った割に「コレ?」という気もします。果たして、128次元のデータの3倍、384次元のデータへの圧縮でこれは変わるのでしょうか。
圧縮後384次元、エポック数100のニューラルネットワークモデルの学習
次に、圧縮後の次元数が384(=3072÷8)となるニューラルネットワークモデルで学習を行います。このモデルは次のようにして作成しています。
encoder = torch.nn.Sequential(
torch.nn.Linear(input_size, input_size // 2),
torch.nn.ReLU(),
torch.nn.Linear(input_size // 2, input_size // 4),
torch.nn.ReLU(),
torch.nn.Linear(input_size // 4, input_size // 8)
)
decoder = torch.nn.Sequential(
torch.nn.Linear(input_size // 8, input_size // 4),
torch.nn.ReLU(),
torch.nn.Linear(input_size // 4, input_size // 2),
torch.nn.ReLU(),
torch.nn.Linear(input_size // 2, input_size),
torch.nn.Tanh()
)
net2 = AutoEncoder2(encoder, decoder)
このニューラルネットワークモデルを先ほどと同様なコードで学習させてみると、3時間弱の時間が必要でした。圧縮後の次元数が多く、その途中の全結合層の重みやバイアスも増えているので(デコーダー部も同様)、これはしょうがないことでしょう。とはいえ、待つ身としてはちょっとしんどいところではあります。筆者は上に述べた3回の学習が行われるようにGoogle Colabでコードを書いておいて、実行ボタンをクリックして、寝ちゃいました。が、起きてもまだ全てが完了してはいませんでした。
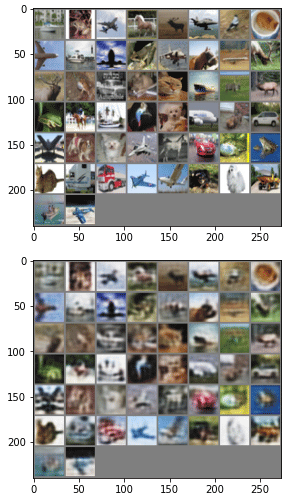
そんなヨタ話は置いておいて、先ほどと同様に、最後に学習を行った結果とその元画像を以下に表示します。
ひいき目に見て、次元圧縮後のデータが128次元のものよりは鮮明になっているような気がします(気がするだけかもしれませんが)。実際にどうかは、3回の学習が終わったところで、テスト用データをそれぞれのニューラルネットワークモデルに入力して、その画像を一覧してみることにしましょう。
圧縮後384次元、エポック数が計300のニューラルネットワークモデルの学習
次に、上で100エポックの学習を終えたニューラルネットワークモデルを使って、さらに200エポックの学習を行いました(計300エポック)。その結果を以下に示します。
これは他の2つよりもかなりきれいに復元できているように見えます。つまり、100エポックだけではまだ学習は十分でなかったといえるでしょう(となると、128次元の方でも学習を進めれば、それなりの結果が得られる可能性はあるということです。が、そこまで試す時間と気力がなかったので、これについては放置しておきます)。
なお、こちらは学習が終わるまでに6時間弱かかったことも報告しておきましょう。
ここまでの結論としては次のようになります。
- 圧縮後の潜在変数の次元数が多い方が復元された画像の精度も高くなる
- 今回の実験に関しては、100エポックの学習よりも300エポックの学習の方が復元された画像の精度が高くなる
こう書いてみると「当たり前」のことのような気がしてきましたが、そうしたことを確認するのが本連載の目的です。この先があるとすれば、圧縮後の次元数はどのくらいが適切なのか、学習はどこまで進めればよいか、といったことをもう少し踏み込んで調べることになるのでしょうが、ここではおおよその方向性が出たところでよしとすることにします。
テストデータを使った画像の復元
3つ(というか、2つ)のニューラルネットワークモデルの学習が終わったところで、テストデータをそれらに入力して復元された画像を比較してみることにします。
実際のコードは今回のノートブックを参考にしてほしいのですが、実は学習が終わるたびに次のようなコードを使って、学習が終わった時点でのニューラルネットワークモデルを保存してあります。
torch.save(net, '128epch100.pt') # 他のモデルも同様
torch.save関数は、ディスク上のファイルにPyTorchのオブジェクトを保存するものです。これらを読み込むにはtorch.load関数を使います。ここでは、以下のようにして、保存しておいたニューラルネットワークモデルを3つの変数に読み込みました。なお、ファイル名は「圧縮後の次元数epchエポック数.pt」としてあります。
model1 = torch.load('128epch100.pt')
model2 = torch.load('384epch100.pt')
model3 = torch.load('384epch300.pt')
変数model1には1つ目の学習で使ったものが代入されます。変数model2に代入されるのは2つ目の学習が終わった時点のモデルで、変数model3はさらに200エポックの学習を行った時点のモデルです(これら2つはもともとのオブジェクトとしては同一で、学習により重みやバイアスが異なるものとなっています)。
また、テストローダーは冒頭のコードで既に定義済みなので、以下のコードでその先頭5要素を取り出して、上で読み込んだニューラルネットワークに入力しています。
iterator = iter(testloader)
img, _ = next(iterator)
out1 = model1(img.reshape(-1, 3 * 32 * 32))
out2 = model2(img.reshape(-1, 3 * 32 * 32))
out3 = model3(img.reshape(-1, 3 * 32 * 32))
この後は次のコードでニューラルネットワークモデルに入力した画像と、それぞれが復元した画像を表示してみます。「plt.figure(figsize=(8, 8))」というのは、画像のサイズを少し大きくするために使っています。
plt.figure(figsize=(8, 8))
imshow(img)
plt.figure(figsize=(8, 8))
imshow(out1.reshape(-1, 3, 32, 32))
plt.figure(figsize=(8, 8))
imshow(out2.reshape(-1, 3, 32, 32))
plt.figure(figsize=(8, 8))
imshow(out3.reshape(-1, 3, 32, 32))
その結果は次の通りです。
一番上は元のテストデータ画像です。その下が圧縮後128次元で100エポックの学習をしたニューラルネットワークモデルのもの、そして圧縮後384次元で100エポックの学習をしたニューラルネットワークモデルのもの、最後が圧縮後384次元で300エポックの学習をしたニューラルネットワークモデルのものです。復元された画像は上から下へとよい結果になっていることが(画像と同じく薄ぼんやりと)分かるのではないでしょうか。
最後の画像は他のものよりはよいですが、これをさらにクッキリとした画像にするのはたいへんそうです(圧縮後の次元数を多くすれば、圧縮の意味がなくなり、学習をさらに進めるのであれば、より多くの時間がかかるようになります)。
画像の復元の度合いに加えて、以下に実行にかかった時間と学習完了時の平均損失を表にまとめておきます。
| モデル | 完了までにかかった時間 | 最終的な平均損失 |
|---|---|---|
| 圧縮後128次元/100エポック | 1時間半弱 | 0.03530 |
| 圧縮後384次元/100エポック | 3時間弱 | 0.02564 |
| 圧縮後384次元/300エポック | 6時間弱 | 0.01669 |
| それぞれのニューラルネットワークの学習にかかった時間と最終的な平均損失 | ||
最後のモデルは2つ目のモデルで100エポックの学習が完了してからさらに6時間かかっているので、実際には300エポックの学習には8〜9時間が必要だったということです。また、平均損失については以前の学習を引き継いでいるので、より小さな値になるのは当たり前といえば当たり前ではあります。平均損失については最初のモデルと2つ目のモデルとで、同じエポック数でも差がそれなりに出たことの方が重要でしょう。このことからも、圧縮後の次元数は少ないよりは多い方が画像の復元がうまくいくことが示唆されているといえるでしょう。
とここまで、全結合型のニューラルネットワークを使って、CIFAR-10の画像データのエンコード/デコードを見てきました。しかし、ここまでにグズグズといってきたように、これでは学習に時間がかかりすぎです。もっと効率のよい方法があるはずです。例えば、本連載のMNISTの手書き数字の認識ではCNNと呼ばれるニューラルネットワークを使いました。もしかしたら、オートエンコーダーでもこれを利用できるかもしれません。というわけで、ホントはここでCNNを用いた「畳み込みオートエンコーダー」の話に進もうと思ったのですが、それは次回の話題としましょう。
Copyright© Digital Advantage Corp. All Rights Reserved.

 実行結果
実行結果


