第9回 機械学習の評価関数(回帰/時系列予測用)を使いこなそう:TensorFlow 2+Keras(tf.keras)入門
回帰問題や時系列予測で使える代表的な評価関数をまとめ、使い分け指針を示す。平均絶対誤差(MAE)、平均二乗誤差(MSE)とその平方根(RMSE)、平均二乗対数誤差(MSLE)とその平方根(RMSLE)、平均絶対パーセント誤差(MAPE)、平均二乗パーセント誤差の平方根(RMSPE)を解説。回帰分析用の決定係数にも触れる。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
前々回は回帰問題、前回は分類問題の解き方を解説した。それぞれの評価時における精度指標(Metrics)として、回帰問題では平均絶対誤差(MAE)を、分類問題では正解率(Accuracy)を用いた。これらは、最も基礎的で一般的な評価関数(Metric function)である。実践では、より多様な評価関数を使い分けることになるだろう。
そこで今回は、回帰問題や時系列予測(後述)で使える代表的な評価関数をまとめる。具体的には、下記の7つの評価関数を説明する。
本稿は、一通り目を通すことでざっくりと理解したら、あとは必要に応じて個別に参照するという「辞書的な使い方」を推奨する。といっても、上記の順番で違いを意識しながら理解すればそれほど難しくはないので安心してほしい。
時系列予測について
本連載では、ここまで回帰(Regression)と分類(Classification)については説明してきたが、「時系列予測」は今回が初出である。よって最初に、時系列予測について簡単に説明しておこう。
時系列予測(Time-series forecasting)とは、年/月/日/時/分といった周期性/季節性のある過去データから機械学習モデルを作成し、それを使って入力した期間から次の期間を(未来)予測することである。言葉では分かりづらいと思うので図で示そう。図1は、TensorFlow公式ドキュメント「時系列予測」のサンプルに従い、マルチステップ(=「次の1つ」ではなく、「次の何個か」という期間予測)のRNN(再帰型ニューラルネットワーク)モデルを作成して、その学習済みモデルを使って2つほど時系列予測してみた結果である。
図1の青色の線が「入力した期間」である。それに続く緑色の点線が「次の期間」の正解値(ラベル)。もう一方のオレンジ色の点線が「次の期間」の予測結果だ(ちなみに、この例ではあまり精度は高くないようだ……)。このような時系列予測は、株価の予測や、物品の販売予測など、表集計されるビジネスデータを中心に広く活用されている。
以上のことから分かるように、時系列予測は回帰の特殊バージョンといえる。そのため、評価関数も回帰用のものがそのまま使える。一方で、例えばMAPE(詳細後述)など、時系列予測でのみよく使われるものもある。そういった個別の事情については、次に述べる「使い分け」や、個々の解説の中で言及することにしよう。
二乗単位(MSE/MSLE)と、元の単位(MAE/RMSE/RMSLE)と、パーセント(MAPE/RMSPE)の使い分け
個別内容の説明に入る前に、上記7種類の評価関数をざっくりと分類し、使い分け指針を示しておこう。
本連載第7回の回帰問題では、
平均二乗誤差('mse')は、誤差を距離に換算する際に誤差を二乗する処理を行うため、実際の数値と単位が異なってくる。一方、平均絶対誤差('mae')はマイナスをプラスに変えているだけなので単位自体は変わっていない。
という文章で、MSE(平均二乗誤差)とMAE(平均絶対誤差)の違いを説明した。それに基づくと、「人間が評価する段階では、MSEよりもMAEの方が扱いやすい」といえるだろう。
これと同じ理屈で、二乗単位のMSEに対して平方根(√)を取って元の単位に戻すのがRMSE(Root MSE:平均二乗誤差の平方根)である。損失関数でMSEを使って最適化した場合に、評価時はその平方根であるRMSEにする方が、MAEよりも自然だろう。そういったこともあり、RMSEは回帰問題の評価時に非常によく使われている(という印象が筆者にはある)。ただし(詳細は後述するが)、解釈性を重視する場合や、外れ値の影響を低減したい場合は、RMSEよりもMAEの方がよい。
MSLE(平均二乗対数誤差)とRMSLE(平均二乗対数誤差の平方根)も、MSEとRMSEの関係と同じで、二乗単位か元の単位かが異なる。また、MSLEとMSEの違いは「L=Logarithmic:対数」を使うかどうかである。(詳細は後述するが)底が同じ対数同士の引き算は1つ対数の割り算になるので、「正解値/予測値」の比率に着目することになる。例えば予測値が1だったり10000だったりするような極端な幅がある場合は、MSE/RMSEではなく、比率に着目するMSLE/RMSLEを使う方が適切である。また、図2は自然対数(ネイピア数eを底とする対数)のグラフ例だが、これを見ると分かるように、特にxの値(=正解値や予測値)が大きくても、yの値(=対数の計算値)はあまり大きくならないという特徴がある。この特徴から、「正解値よりも予測値が大きいときには、あまり大きなペナルティを課したくない(小さいときには課したい)」という場合に、MSLEとRMSLEは適している。
以上で、「二乗単位(MSE/MSLE)」および「元の単位(MAE/RMSE/RMSLE)」の、ざっくりとした使い分け指針を示した。参考までに、二乗単位と元の単位でどのような違いがあるかが視覚的にも理解できるように、第7回の回帰問題でそれぞれの評価関数の結果の履歴をグラフ化してみた。図3を見ると、やはり元の単位の方が分かりやすいようである(※誤差が小数点以下なので、二乗単位の方はより小さい評価値となっている。例えば0.2の二乗は0.04になるので)。
次の「パーセント(MAPE/RMSPE)」は、特に時系列予測でよく使われる評価関数である。先ほどまでの二乗単位や元の単位では、任意の範囲の数値となる。例えば「誤差が0.05」や「12.3」などとなるが、このようにバラバラな数値範囲で示されても、特に一般のビジネスマン向けにはなかなか通じないことがある。そこで「誤差が5%」や「12.3%」などのように、「正解値から見て何%の誤差(ズレ)なのか」をパーセント(元の単位)で示してくれた方が分かりやすいだろう。このニーズに応えるのが、MAPE(平均絶対パーセント誤差)やRMSPE(平均二乗パーセント誤差の平方根)なのである。いずれも単位は(二乗単位ではなく)元の単位である点にも留意してほしい。
例えば「売り上げ予測」などのケースで、10万円の売り上げにおける1万円の誤差と、1000万円の売り上げにおける1万円の誤差がある場合、「誤差1万円です」というのは分かりづらいだろう。「10%の誤差です」や「0.1%の誤差です」の方がより分かりやすい。また、例えば「株価の予測」の場合、期間によって100円、1万円と大きく変動している可能性があったり、銘柄ごとに金額の幅が大きく異なる可能性があったりする。こういったケースでは、パーセントで評価する方が好ましい。
ただしMAPE/RMSPEは、「正解値と予測値の差」を「正解値」で割るため、正解値が0だと割り算ができなくてエラーになる問題がある(※TensorFlow/Kerasの場合、tf.keras.backend.epsilon極小値(例:1E-07=0.0000001)より小さい値は、その極小値にクリッピング=収めることでエラーを回避している)。また、正解値が例えば0.05のように小さい値の場合、誤差のパーセントが非常に大きくなることがとても多いため、あまり向いていない。こういった点でMAPE/RMSPEは、あらゆる評価時に使えるとは限らず、利用可能かどうかはケースバイケースで見極める必要がある。
ニューラルネットワーク(回帰問題/時系列予測)では、以上で説明した「二乗単位/元の単位/パーセントの評価関数」の使い分け指針をざっくりと覚えておけばよい。なお、回帰用の評価関数としては「決定係数 R2」という指標も説明されることがある。これは(重)回帰分析/線形回帰用の評価関数である。重回帰分析は統計学の多変量解析の一手法ではあるが、機械学習の手段として使われることもある。TensorFlow/Kerasで重回帰分析することも不可能ではないが、シンプルな計算なので、多くの機械学習の手法に対応していて手軽に扱えるscikit-learnを使うことをお勧めする。scikit-learnのscore()メソッドで決定係数は難なく算出できる。
以上の使い分け指針を踏まえた上で、それぞれの評価関数の内容と、対応するTensorFlow/KerasのAPIについてさらに詳しく解説していく。
平均絶対誤差(MAE:Mean Absolute Error)
各データに対して「正解値と予測値の差(=誤差)」*1の絶対値を計算し、その総和をデータ数で割った値(=平均値)を表す。
*1 差であればよいので、「正解値−予測値」と「予測値−正解値」のどちらでもよい。以下で紹介する式でも同様。
MAEは、シンプルな評価関数としてよく用いられ、実際に本連載の第7回でも使用した。前述の通り、MSE(平均二乗誤差)の単位問題を回避する目的で使える利点があり、人間にとってシンプルで理解しやすい。解釈性を重要視するならば、回帰問題では後述のRMSEではなくこのMAEを使えばよい。またMAEは、RMSEよりも外れ値の影響を受けにくいという利点もある。
欠点として、絶対値は数学計算で条件分岐が発生して数式が2つに分かれてしまう問題があり、特にその分岐地点では数学的に「微分不可能」になるという問題がある。また、後述のRMSEのように、誤差が大きくても、それほど過大には評価してくれないので、より評価しづらい指標ともいえるだろう。
TensorFlow/Kerasでは、
もしくは(compile()メソッドの引数metricsで)、
- 'mean_absolute_error'
- 'MAE'
という文字列を使えばよい(※損失関数にも同名のものが用意されているので注意)。
平均二乗誤差(MSE:Mean Squared Error)
各データに対して「正解値と予測値の差(=誤差)」を二乗した値を計算し、その総和をデータ数で割った値(=平均値)を表す。
MSEは、最も一般的な損失関数でもあるため、そのまま評価関数としても用いられる。
利点としては、誤差が大きいほど過大に評価する(=間違いをより重要視する)ので、より差を付けて評価しやすくなる(損失関数として見るなら学習しやすくなる。ただし外れ値に敏感になるので、損失関数として利用する場合は外れ値にも過剰適合(=過学習)してしまう問題もある)。
欠点としては、誤差を二乗していること、つまり単位が変わってしまっており、人間にとっては単純に理解しづらいことが挙げられる。この単位問題を回避するためには、絶対値を使う方法(前述のMAE)か、ルート(√)を使って二乗した単位を元の単位に戻す方法(後述のRMSE:Root MSE)が考えられる。
TensorFlow/Kerasでは、
もしくは(compile()メソッドの引数metricsで)、
- 'mean_squared_error'
- 'MSE'
という文字列を使えばよい(※損失関数にも同名のものが用意されている)。
平均二乗誤差の平方根(RMSE:Root Mean Squared Error)
平均二乗誤差(MSE)の平方根 √(ルート:Root)の値を表す。
※他の用語に倣い、上から訳していくと「平方根(Root)平均(Mean)二乗(Squared)誤差(Error)」となるが、「MSEで二乗された単位を√で元に戻した」という意味/意図がよりよく伝わるように「平均二乗誤差の平方根」と本稿では表記している。RMSEは「二乗平均平方根誤差」「平均二乗誤差平方根」「平均平方根二乗誤差」などとも呼ばれている(RMSEと呼ぶ方が通じやすい)。
RMSEは、平均二乗誤差(MSE)の単位問題を回避するため*2の評価関数として利用できる。回帰問題の評価時には、基本的にRMSEかMAEのどちらかを使えばよい。
*2 ちなみに、MSEは統計学の「分散」の計算方法に似ているが、RMSEは「標準偏差」の計算方法に似ている。このことは、両者の計算式を混同しないためにも予備知識として知っておいた方がよい(※統計学では「正解値と予測値の誤差」ではなく「各データと平均値の偏差」を用いる点が異なる)。単位問題を回避するという視点では、標準偏差も分散の二乗された単位を元に戻しているものと考えられる。
利点はMSEと同じになるが、誤差が大きいほど過大に評価する(※RMSEがMAEよりも小さい値になることはない。図4を見ると、青色のRMSEの線は、緑色のMAEの線よりも常に上にある)ので、より差を付けて評価しやすくなる。ただし外れ値に敏感になるので、それが問題となることもある。
欠点としては、評価対象のサンプルサイズ(=データ数)が多いほど、RMSEはMAEよりもますます大きな値になる傾向にある点に注意が必要なことだ。どういうことかいうと、「サンプルサイズの違うデータ間では、RMSE値をそのまま比較することはできない」ということである(※MAEであれば比較できる)。
TensorFlow/Kerasでは、
- tf.keras.metrics.RootMeanSquaredErrorクラス(ちなみにRootMeanSquaredError(name='rmse')でインスタンス生成すると「rmse」という短縮名でログ出力できて便利)
もしくは(compile()メソッドの引数metricsで)、
- 'root_mean_squared_error'
- (※短縮表記なし)
という文字列を使えばよい。
平均二乗対数誤差(MSLE:Mean Squared Logarithmic Error)
各データに対して「正解値の対数と予測値の対数との差(=対数誤差)」を二乗した値を計算し、その総和をデータ数で割った値(=平均値)を表す。
数式を見ると、log(1+yi)という形で「+1」しているが、これは「log(0)=マイナス無限大」となって計算できないのを回避するためだ。また、自然対数(eを底とする対数)ではlog(1)=0となるからである(※前掲の図2と、「+1」した図5を見比べると分かる)。なお、正解値や予測値は-1より大きい必要がある。「+1」しているため、正解値や予測値が0であっても問題ない。
MSLEは、損失関数にもなり、そのまま評価関数としても用いられる。
MSEと比べてMSLEは、(前述の使い分けでも説明したように)対数の性質上、正解値や予測値(図5のx)が大きくなっても自然対数計算した値(図5のy)はあまり大きくならない。よって誤差の範囲が極端に幅広い場合にも対応できるという利点があるのだ。
欠点としては、誤差を二乗していること、つまり単位が変わってしまっており、人間にとっては単純に理解しづらいことが挙げられる。この単位問題を回避するためには、ルート(√)を使って二乗した単位を元の単位に戻す方法(後述のRMSLE:Root MSLE)が考えられ、実際に評価関数としては、MSLEよりもRMSLEの方がよく用いられている。
TensorFlow/Kerasでは、
もしくは(compile()メソッドの引数metricsで)、
- 'mean_squared_logarithmic_error'
- 'MSLE'
という文字列を使えばよい(※損失関数にも同名のものが用意されている)。
平均二乗対数誤差の平方根(RMSLE:Root Mean Squared Logarithmic Error)
Copyright© Digital Advantage Corp. All Rights Reserved.
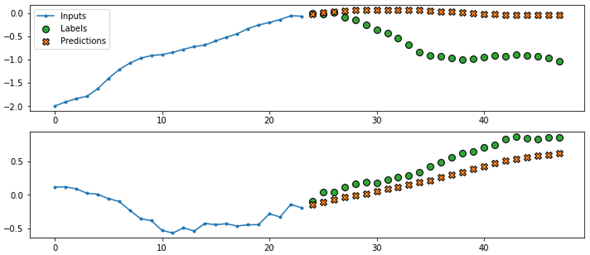
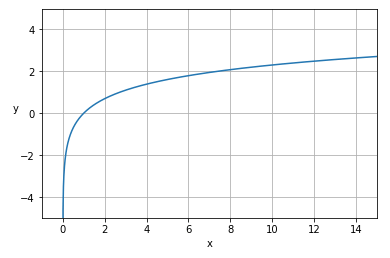 図2 自然対数のグラフ例
図2 自然対数のグラフ例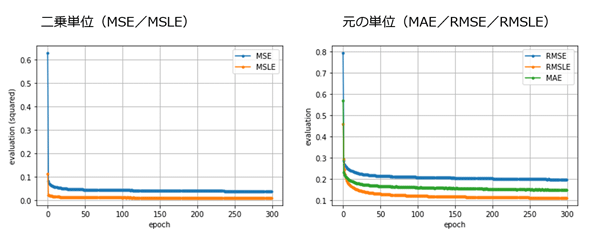



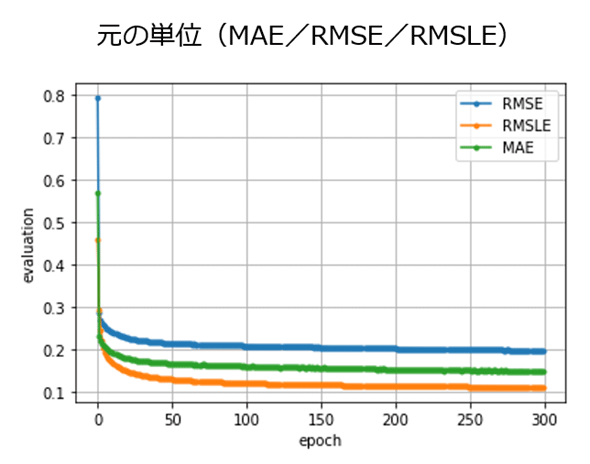

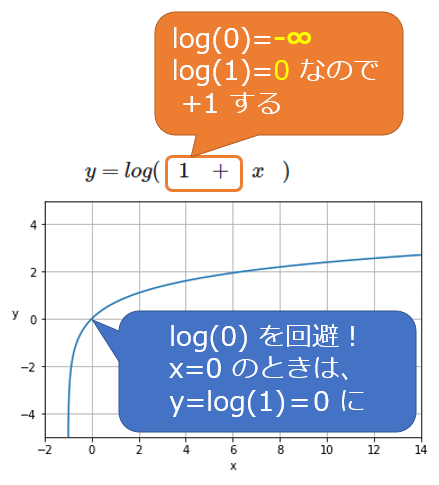 図5 y=log(1+x)の自然対数グラフ
図5 y=log(1+x)の自然対数グラフ


