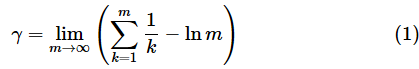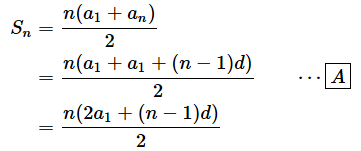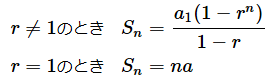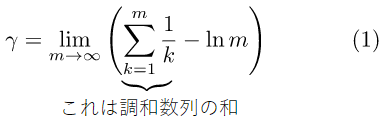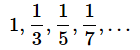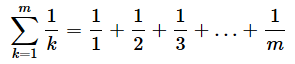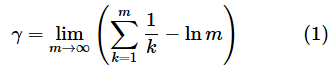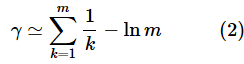中学・高校数学でオイラーのγの近似値を求めるプログラミング：数学×Pythonプログラミング入門（1/2 ページ）

調和数列を使ってオイラーのγ（ガンマ）の近似値を求める問題を通して、Σを使った総和の計算をプログラミングする。また、Pythonのリストや繰り返し処理についてまとめ、身近な事例を使って、繰り返し処理の制御変数とリストのインデックスをどう対応させるかという問題について考える。

連載目次

　前回は、ウオーミングアップの回として、フェルマーの小定理やアンドリカの予想、超球の体積といったトピックを通してPythonプログラミングの初歩を振り返りました。

　今回から、数式などの「数学の言葉」で表された問題をプログラムとして記述していくことに本格的に取り組んでいきましょう。

　まず、調和数列を使ってオイラーのγ（ガンマ）と呼ばれる値の近似値を求める問題を例に、Σ（総和）の計算をプログラミングするために使われるお決まりのパターンを見ていきます。さらに、繰り返し処理を行うときに最もつまずきやすいポイント――繰り返し処理の制御変数とリストのインデックスをどう対応させるかという問題――について、可処分所得の対前年度比の計算などの身近な例を使って考えていきます。

　練習問題としては、ネイピア数（自然対数の底e）の近似値を求める例、2つの変数の共分散を求める例、株価のn日移動平均を求める例を取り上げます。

連載：

『数学×Pythonプログラミング入門 ― 中学・高校数学で学ぶ』

この連載では、中学や高校で学んだ数学を題材にして、Pythonによるプログラミングを学びます。といっても、数学の教科書に載っている定理や公式だけに限らず、興味深い数式の例やAI／機械学習の基本となる例を取り上げながら、数学的な考え方を背景としてプログラミングを学ぶお話にしていこうと思います。

羽山博

筆者紹介： IT系ライター、大学教員（非常勤）。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く98回で一旦中断。

目標： オイラーのγの近似値を求める

　オイラーという数学者はあまりにも有名なので、そんな名前は聞いたことがない、という人はほとんどいないのではないでしょうか。世界で最も美しいと言われるオイラーの関係式（e^iπ＝−1） にも登場しますし、身近なところでは「一筆書きできる道」はオイラー閉路と呼ばれます。しかし、オイラーのγ（ガンマ）（またはオイラーの定数）と呼ばれる値はあまり知られていないかもしれません。

　オイラーのγは以下のような値ですが、実は、この値の性質はまだよく分かっていません。しかも、無理数なのかどうかもいまだに分かっていません（ちなみに、前回取り上げたガンマ関数のx＝1における微分係数Γ'(1) と−γが等しくなります。数学は不思議だらけですね）。

　この値を求めるための数式は以下の通りで、調和数列と自然対数が使われています。

　オイラーのγは、AI／機械学習ですぐに使うような値ではありませんが、数式をプログラミングしていくための基本的なパターンを含んでいるので、このプログラミングに取り組むことは、AI／機械学習だけでなく、どのような計算をする場合にも、そのための基礎を養うのに役立ちます。

　さて、この数式をプログラムとして表すことを考えていくわけですが、Σが総和を表すことが分かっても、式の中に書かれている∞（無限大）の扱いに困りますね。プログラムで無限に足し算を行うことはできないからです（永遠に答えが求められませんから）。そこで、近似値を求めるためにmに好きな値（ある程度大きな値）を指定するものと考えてください。

　では、コードを書いてみてください。……と言いたいところですが、いきなりそう言われてスラスラとできる人は多くはないかと思います（いや、これぐらいなら楽勝だよ、と思った方はぜひ独力で取り組んでみてください。答え合わせはこちら）。もしかすると「ホントに中学／高校数学の範囲なの？」と思われる方もいるかもしれませんね。しかし、間違いなく中学／高校の知識だけで理解できる数式です。そこで、この数式を理解するために、以下の内容についておさらいしておきましょう。（1）式を見て、ちょっと「ビビった」という人もご心配なく。一歩ずつゆっくり進めるので必ず理解できます。

　なお、これらの内容について、既に十分に理解しているのでおさらいなんて必要ないという方は、2章まで読み飛ばしてもらって構いません。では、数列から見ていきましょう。

1. 数列のおさらいをかねたサンプルプログラム

　数列とは、a₁,a₂,...,a_nという数の並びです。これを簡単に{a_n}と表すこともあります。

（例）

　これらの例では、値がどう並んでいるかというルールはよく分かりませんが、数が並んでいるわけですから、レッキとした数列です*1。ただし、高校数学では、等差数列や等比数列などのルールが決まったものだけを数列と呼んでいるようです。それらのルールは以下の通りです。

　等差数列と等比数列の例を見ておきましょう。

　等差数列や等比数列にはルールがあるので、上のように数字を並べるのではなく、ルールを数式で表しておいた方が正確で、応用の幅も広がります。等差数列の第n項の値つまりa_nは、初項をa₁、公差をdとすると、以下のように表されます。

　念のため確認しておきましょう。以下、穴埋めになっているのでちょっと考えてみてください。オレンジ色の部分をクリックすると答えが表示されます。例えば、上の例で3番目の奇数にあたる値は、初項a₁＝1、公差d＝2、n＝3なので、

　　a₃ ＝ 　1　 ＋ (　3　−1)× 　2　 ＝ 5

となり、ちゃんと第3項の5が求められます。

　一方、等比数列の第n項は公比をrとすると、以下のようになります。

　こちらも、上の例で確認しておきましょう。3番目の項は、初項a₁＝100、公比r＝1.01、n＝3なので、

　　a₃ ＝ 　100　× 　1.01　^3　−1 ＝ 102.01

となり、ちゃんと第2項の102.01が求められました（初項に預金額を、公比に1＋利率を、nに利払い回数を指定すれば、定期預金の元利合計の計算ができますよ）。

　では、ルールが分かったところで、軽くウオーミングアップといきましょう。奇数の自然数を1から10個分、リストとして返す関数を作ってみてください。なお、これ以降のサンプルプログラムについては作成から実行までの流れを動画で見られるようにしてあります。以下の例を含めて、プログラミングに不慣れな方に向けての動画はこちらにまとめてあるのでぜひ参考にしてください。

　「初項をaという変数で表して1を代入する」「公差をdという変数で表して2を代入する」といった具合に、数式で表されている内容を一つ一つ丁寧にコードとして書いていきます。以下のリスト1では、できるだけ公式がそのままの形で表されるようにコードを書いてみました。空欄になっている箇所（_____の部分）を埋めてみてください。

　各行の末尾にある#以降の文章はコメントなので、プログラムの実行には影響を及ぼしません。実際にコードを入力するときには、コメントの入力は省略してもらっても構いません（が、必要に応じて書いておいた方が、コードが分かりやすくなります）。

　では、答えを記しておきましょう。

（答え）　　a + (n-1)*d　

　公式のままですね。

【まとめ】for文による繰り返し、range関数による値の並びの作成

　for文の書き方やrange関数の使い方にはちょっと注意が必要です。既にfor文やrange関数になじんでいる方はこのまとめは読み飛ばしてもらっても構いません（でも、意外な発見があるかもしれないので、斜め読み程度には目を通しておいてもらうのがいいと思います）。

　例によって、ここでは必要最小限のまとめと、数学との関連、留意点のみに絞って説明しているので、Python文法のより詳細な内容については、『Python入門』をご参照ください。

　では、for文の書き方を簡単な例で図解してみましょう。

図1　for文の書き方
for文ではinの後に書かれた値の並びから値を1つ取り出して変数に代入し、文を実行する。続いてまた値の並びから値を1つ取り出して変数に代入し、文を実行する。このような処理を繰り返し、値の並びから取り出せるものがなくなったらfor文を抜け、次に進む。for文の1行目の最後の:を忘れないように。また、繰り返して実行したい文はインデント（字下げ）してfor文の範囲内にあることを表す。

　続いて、range関数の使い方です。range(a, b)とすると、a以上、b未満の整数を表す値の並び（rangeオブジェクト）が得られます*2。b以下ではなくb未満であることに注意してください。なお、aを省略してrange(b)とすると、0以上、b未満となります。

　図1のコードを実行するとどういう結果になるでしょうか。range(0, 5)は、0以上5未満なので、iには順に0, 1, 2, 3, 4が代入され、それらの2乗つまり、0, 1, 4, 9, 16が順に出力されます。

　ところで、range関数は、range(a, b, c)のように指定すると「cずつ増やす」という意味になります。従って、リスト1の奇数のリストは以下の1行のコードで作成することもできます。

　実は、range関数はまさに等差数列を作るための関数なのです。ただし、作成できるのは整数の等差数列に限ります。従って、どの引数にも0.5などの小数部がある数値は指定できません。

　なお、for文の後にはrange関数だけでなく、リストや文字列などを指定することもできます。以下のコードを実行すれば、最初に見たAppleの株価が2021年8月5日〜11日の間に結局どれだけ上下したかが計算できます。

　リスト3は合計を求めるためのお決まりのパターンです。最初に合計を求めるための変数に0を入れておき、繰り返し処理の中で値を次々と足していくというわけです。これについては、後でもう一度説明します。

2. 調和数列の和を求めるプログラム

　続いて、数列の和を求めるプログラムを見ていきます。と言っても、等差数列や等比数列の第n項までの和を求める場合は公式が使えるので、単純にそれらの公式を使って計算すれば済みます。ここではこれ以上詳しく取り扱いませんが、一応、公式だけ記しておきます。なお、数列の和のことを級数と呼ぶこともあります。

　［A］では、1章で見たa_nを求める公式を代入しています。

　さて、いよいよここからが本題です。大事なのでもう一回、言っておきましょう。ここからが本題です。目標のところに示した数式の一部は調和数列と呼ばれる数列の和になっています。

　調和数列とは、等差数列の逆数を並べた数列です。例えば、以下のような数列が調和数列です。

　この例は、1以上の奇数の数列（初項1、公差2の等差数列）の逆数の数列です*3。

　さて、（1）式の中に含まれている調和数列の和は、自然数（初項1、公差1の等差数列）の逆数の数列の和になっていることが分かりますね。その部分だけを取り出して、どのような計算をしているのかが分かるように足し算で表してみましょう。

　実は等差数列や等比数列と違って、調和数列には和を求める公式がありません。そのため、最初から各項を順に足していくしかありません。しかし、このことは、Σによる総和の計算をプログラミングするということにほかなりません（と、大げさに言いましたが、基本中の基本です）。ここでは、初項から第100項までを足してみましょう。もちろん、+演算子で100個の項をつなぐわけではなく、繰り返し処理を使います。

3.　オイラーのγの近似値を求めるプログラム

　2章で見た調和数列の和は、mの値をどんどん大きくすると、無限大に発散することが分かっています。しかし、最初に見た以下の式は、オイラーのγ（＝0.5772156...）に収束します。

　前述したように、プログラムで無限に足し算を行うことはできないので、近似値を求めるためにmに好きな値を指定して計算できるようにしましょう。従って、limの部分（mの値を無限大に近づけていく）は気にしなくてもいいということになります。式は以下のようになりますね。

　なお、lnというのはlog_enのことです。eを底とする対数（自然対数）はよく使われるので、lnと略して書くことがよくあります（lnはlog naturalの略です）。また、（2）式の≃は「ニアリーイコール」と読み、ほぼ等しいということを表します。ともあれ、これならリスト5を少し書き換えるだけでできますね。

　ちゃんと、γ＝ 0.5772156...に近い値になりましたね。ところで、リスト7には無駄が多いと思いませんか。調和数列の和を求める関数は既にリスト5で作っているのだから、それを使えばいいじゃないか、ということですね。そうするなら、コードは以下のように簡単になります。

　次のページでは、Pythonのリストや繰り返し処理についてまとめた後、身近な事例を使って、繰り返し処理の制御変数とリストのインデックスをどう対応させるかという問題について考えます。最後に練習問題を3つ用意しています。