第6回 B木から要素を削除する方法を学ぼう
はやしつとむ
アナハイムテクノロジー株式会社
2009/7/16
オブジェクト指向によって、アルゴリズムは隠ぺいされていることが多くなった。しかし、「用意されていない処理」が求められたときに対応できるだろうか(編集部)
第5回「RDBMSで使われるB木を学ぼう」では、木構造の中でもメジャーなバランス木の一種であるB木(B-Tree)について解説しました。
前回はB木への要素の追加について説明しましたので、今回はB木からの要素の削除を取り上げたいと思います。
本論に入る前に、前回のおさらいとなりますが、B木がどのようなものであるかを確認しておきましょう。
B木はAVL木と同様なバランス木の一種です。B木は、節点に複数のキーを格納できます(これをバケットと呼びます)。そして、新しく追加されるキーは、それぞれのキーに対する大小によって子の節点へと振り分けられていきます。
B木がバランスを保って保持されるためには以下のルールが守られる必要があります。これをK次のB木といいます。
- 各節点は最大で2×K個のキーを保持する
- 根節点以外の各節点は、最小でK個のキーを保持する
- M個のキーを持つ節点はM+1個の子を持つ
- 葉はすべて同じレベルになる
筆者はDelphi 2009でサンプルプログラムを作成していますが、Delphiをお持ちでない方は下記のURLからTurboDelphiをダウンロードして、インストールしてみてください。
| 関連リンク: | |
| Delphiトライアル版/無償バージョン http://www.codegear.com/jp/downloads/free/delphi |
|
 B木からの要素の削除(葉の場合)
B木からの要素の削除(葉の場合)
まず、B木の葉の部分において要素の削除が行われた場合を検討していきましょう。葉の節点からある要素が削除されると、節点の内部で要素の並べ替えが発生します。
図1では、一番左側の葉の真ん中の要素(10)が削除されました。残りの要素(11)を左側へ寄せます。
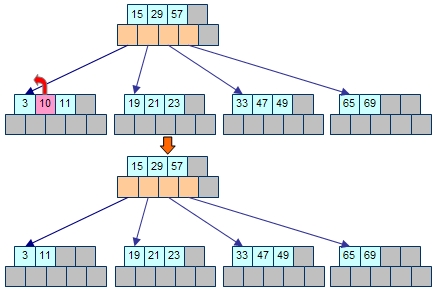
ここで、一番左側の葉節点の要素が2つとなりました。さらに要素をもう1つ削除するとB木のバランスルールを満たせなくなります。つまり、要素数が次数Kを割る場合には、どこかから要素をもらって来る必要があります。
そこで右隣の葉節点との間で要素の数を調整します。まず、親節点の左側の要素(15)をもらい、そこに右隣の葉節点の一番小さい要素(19)を移します。
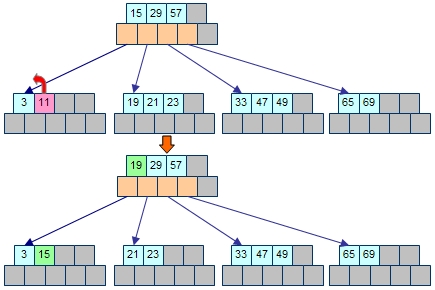
しかし、これでは一番右側の葉節点から要素を削除する場合、困ったことになります。なぜならば、これ以上右側にもらってくるべき要素がないのです。そのため、一番右側の葉節点からの要素の削除だけは左側の葉節点と要素の調節をすることにします。
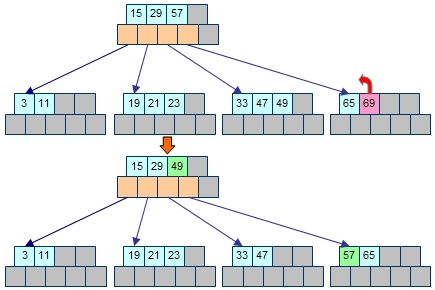
さて、図2の状態になっている一番左側の葉節点から、さらにもう1つ要素を削除することを考えてみます。すでに右隣の葉節点には要素がK個しかありませんから、これ以上、要素を捻出できません。
このような場合には、この2つの葉節点をマージします。2つの葉節点内の要素数の合計は2K-1になるので、ここに親節点の要素を1つ加えて、新しく満杯の節点にまとめてしまいます。
要素を右側の葉節点へとまとめて、左側の葉節点を削除すると考えると、親節点とのリンクがきれいに整理できるのが分かります。
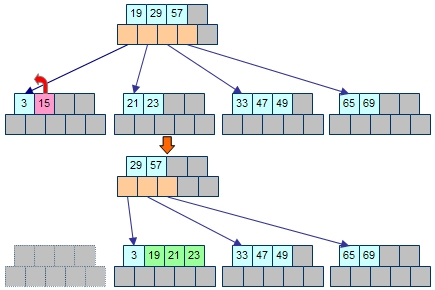
 B木からの要素の削除(葉でない場合)
B木からの要素の削除(葉でない場合)
次に、子の節点がある親節点から要素を削除する場合を検討しましょう。この場合、要素を左右へ振り分けるルール、つまり自分より小さいものは左側、自分より大きいものは右側に振り分けることを考慮すると、AVL木と同じように「左側部分木の一番右側」の要素を削除した要素のところへ持ってくればよいのです。

たとえ木の段数が深かったとしても、左側の部分木の中で一番大きい値を持ってきて、削除した親の要素と入れ替えることで、木全体のバランスを崩さずに済むことが分かります。
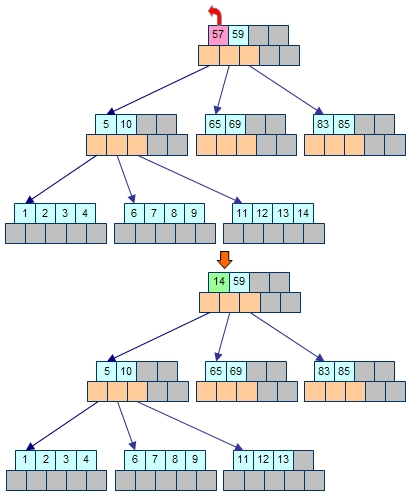
どんどん親節点にある要素を削除してみましょう。
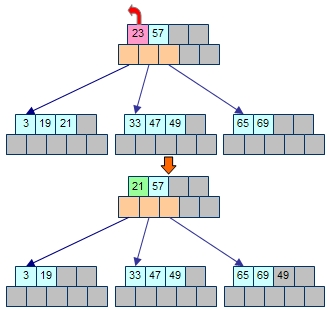
左側部分木から要素を取り出すことができない状態になった場合には、1つ右側の葉節点と要素の調整を行って、融通してもらいます。
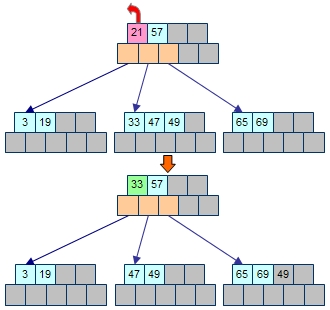
左右の子節点のどちらからも要素を捻出できない状態になった場合には、子節点をマージします。
削除された親節点の要素があったところに、左側の子節点から要素をもらうところまでは、これまでと同じです。ところが、そこで左側の子節点の要素数がB木のルールを満たさなくなってしまうため、親節点に要求して右側の子節点から要素をもらおうとします。しかし、もはや右側の子節点にも融通する余裕がありません。
ここで、両方の子節点のマージが発生します。このとき、先に左側の子節点が差し出した要素を、マージの中間点として親から再度もらい受けることになります。図9でいうところの19が「行って来い」になるわけです。
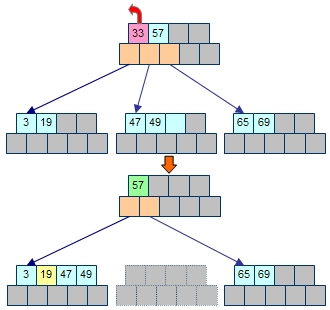
1/2 |
| Index | |
| B木から要素を削除する方法を学ぼう | |
| Page1 B木からの要素の削除(葉の場合) B木からの要素の削除(葉でない場合) |
|
| Page2 B木の高さが低くなる場合 B木への追加も削除もできるテストプログラム |
|
| Appendix BTree.pasのソースコード |
|
| Delphiアルゴリズムトレーニング |
| Coding Edgeお勧め記事 |
| いまさらアルゴリズムを学ぶ意味 コーディングに役立つ! アルゴリズムの基本(1) コンピュータに「3の倍数と3の付く数字」を判断させるにはどうしたらいいか。発想力を鍛えよう |
|
| Zope 3の魅力に迫る Zope 3とは何ぞや?(1) Pythonで書かれたWebアプリケーションフレームワーク「Zope 3」。ほかのソフトウェアとは一体何が違っているのか? |
|
| 貧弱環境プログラミングのススメ 柴田 淳のコーディング天国 高性能なIT機器に囲まれた環境でコンピュータの動作原理に触れることは可能だろうか。貧弱なPC上にビットマップの直線をどうやって引く? |
|
| Haskellプログラミングの楽しみ方 のんびりHaskell(1) 関数型言語に分類されるHaskell。C言語などの手続き型言語とまったく異なるプログラミングの世界に踏み出してみよう |
|
| ちょっと変わったLisp入門 Gaucheでメタプログラミング(1) Lispの一種であるScheme。いくつかある処理系の中でも気軽にスクリプトを書けるGaucheでLispの世界を体験してみよう |
|
- プログラムの実行はどのようにして行われるのか、Linuxカーネルのコードから探る (2017/7/20)
C言語の「Hello World!」プログラムで使われる、「printf()」「main()」関数の中身を、デバッガによる解析と逆アセンブル、ソースコード読解などのさまざまな側面から探る連載。最終回は、Linuxカーネルの中では、プログラムの起動時にはどのような処理が行われているのかを探る - エンジニアならC言語プログラムの終わりに呼び出されるexit()の中身分かってますよね? (2017/7/13)
C言語の「Hello World!」プログラムで使われる、「printf()」「main()」関数の中身を、デバッガによる解析と逆アセンブル、ソースコード読解などのさまざまな側面から探る連載。今回は、プログラムの終わりに呼び出されるexit()の中身を探る - VBAにおけるFileDialog操作の基本&ドライブの空き容量、ファイルのサイズやタイムスタンプの取得方法 (2017/7/10)
指定したドライブの空き容量、ファイルのタイムスタンプや属性を取得する方法、FileDialog/エクスプローラー操作の基本を紹介します - さらば残業! 面倒くさいエクセル業務を楽にする「Excel VBA」とは (2017/7/6)
日頃発生する“面倒くさい業務”。簡単なプログラミングで効率化できる可能性がある。本稿では、業務で使うことが多い「Microsoft Excel」で使えるVBAを紹介する。※ショートカットキー、アクセスキーの解説あり
|
|





