グラフ問題とバルク同期並列の常識をGiraphで体得:ビッグデータ処理の常識をJavaで身につける(5)(1/3 ページ)
Hadoopをはじめ、Java言語を使って構築されることが多い「ビッグデータ」処理のためのフレームワーク/ライブラリを紹介しながら、大量データを活用するための技術の常識を身に付けていく連載
ソーシャル時代の「グラフ問題」の重要性
「グラフ問題」とは、どのようなものか、ご存じでしょうか? ご存じでない方でも実は、「グラフ」を活用したシステムを日常的に使っているのです。
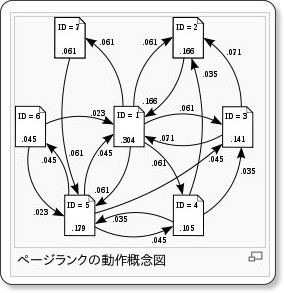
その1つは「Google」「Yahoo!」といった、Webの検索システムです。Webの検索システムでは、検索結果の表示順の判断基準の1つとして、Webページの重要度を示す「PageRank(ページランク)」と呼ばれる指標を用います。このPageRankは「注目に値する重要なWebページは、たくさんのページからリンクされる」「重要なページからのリンクは価値が高い」というような基準でWebページの重要度を評価します。
このPageRankでは、Webページをグラフの頂点(Vertex)、ページのリンクをグラフの枝(Edge)で表現しますが、物事の連携関係をグラフ構造で表現できるものに対し、その構造の評価を行うのが「グラフ問題」です。
このグラフ問題を解決するアルゴリズムは古くから研究されていますが、近年のソーシャルネットワーク/SNSなどの広まりに伴い、グラフ問題で取り扱うデータサイズが劇的に大きくなりました。単一システムでグラフ全体を取り扱うのが処理時間・データサイズ面で困難になりつつあり、グラフを分割し分散環境で並列に処理することが望まれます。
では、グラフ問題をHadoopを用いた並列分散環境で解決することは可能なのでしょうか? それには、グラフ問題に特化した専用のアルゴリズムが必要です。今回は、「Giraph」というソリューションを紹介します。
グラフ問題の解決をMapReduceで試みると
まず、グラフ問題の解決にMapReduceを単純に適用すると、どのような処理になるか、そこにどのような課題が潜んでいるかを見ていくため、「Single Source Shortest Path(SSSP)」問題の解決を試みます。
SSSP問題とは
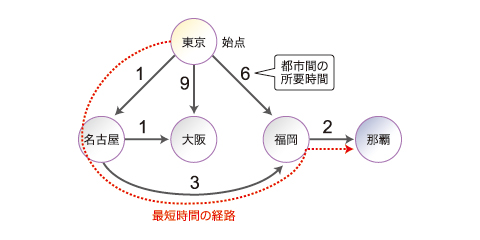
SSSP問題とは、都市間の行き来できる方向(矢印の方向に移動可能)、その所要時間(矢印に付けた数字)が与えられた場合に、ある都市を始点とし、他の都市へ行くための最短時間(あるいは、距離)を求めることです(今回は簡単にするために、最短時間となる経路の算出は検討外とし、これに関する処理は省略しています)。
では、このグラフ構造をMapReduceを用いて解決するには、どのようにデータ表現すればいいのでしょうか? 今回は、各都市の隣接状況をリスト構造で表すKey-Value構造を採用します。
| 表 各都市の隣接状況(始点からの時間:初期状態は始点以外は無限大∞を設定、処理対象:繰り返し処理の収束判定のために使用するフラグ) | ||||||||||||||||||||||||
|
||||||||||||||||||||||||
コラム 2次元配列でも表せる
都市の隣接状況を次のような2次元配列で表す選択肢もあります。
|
|||||||||||||||||||||||
どちらを採用するかは、情報の検索速度、メモリ使用量を検討のうえ、都市の隣接関係がまばらであればリスト構造で情報を保持し、隣接関係が密であれば2次元配列で情報を保持することを考えます。
MapReduce処理の概要
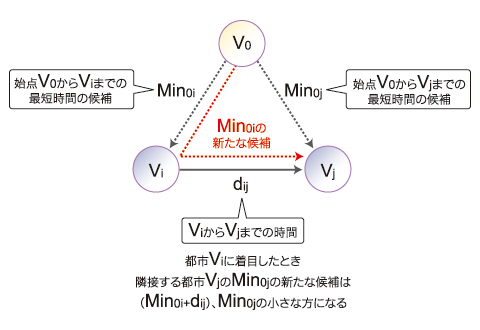
SSSP問題をMapReduceで解決するには、どのような考えを用いればいいのでしょうか? 「隣接する都市に最短時間の候補を伝搬させる」ことを順次繰り返せば、いずれ全都市で最短時間が判明します。
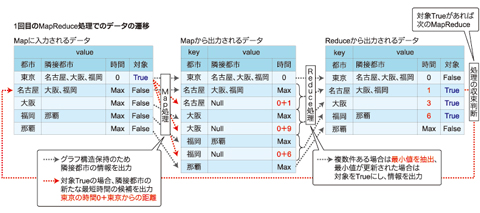
この考えに基づく処理概要を、入出力データの内容とともに示します。
上記表の例では、この処理を4回繰り返せば、全都市の最短時間が求められます。
2つの課題
机上判断では、このようなMapReduceでグラフ問題を解決できますが、実案件に適用するとなると、取り扱う都市数が大きくなるとともに、2つの性能面の課題点が顕在化し、実用に耐えなくなります。
1つは、隣接都市へのデータの伝達においてHDFSを使用することに起因する、処理コストが無視できないということです。MapReduce処理の繰り返しよる、Jobの起動/停止、HDFSアクセス、Shuffleのコストや、グラフ構造を入出力データとして保持する必要性によるCPU、メモリ消費のコストがあります。
もう1つは、解の厳密性がどこまで望まれるのかということです。「MapReduce処理の概要」の項で「いずれ」と述べましたが、MapReduceの繰り返しの収束を何を基準に判断すればいいのでしょうか? 今回のロジックでは、「対象がすべてFalseになれば処理が収束した」と判断しますが、それには1回のMapReduceの終了のたびにHDFSのデータ検索を行い、その条件判断を行う処理コストが必要になります。
また、次のような場合まで厳密解が必要かを考えてみてください。
ソーシャルネットワーク/SNSの世界では「人は自分の知り合いを6人以上介すと世界中の人々と間接的な知り合いになれる」という仮説「六次の隔たり」があります。SSSP問題でも、6回のMapReduce処理を行えば、あらかたの解が得られ、処理の収束判断が不要と割り切ることもできるのではないでしょうか。
このように、MapReduceでの単純な解決は現実的ではなく、グラフ問題の特性を検討する必要があります。
これに対しては、Hadoop Summit 2010の「Design Patterns for Efficient Graph Algorithms in MapReduce」で、効率的なアルゴリズムが紹介されていますが、簡単なグラフ問題にのみ適応可能とのことなので、今回は視点を変え、「Pregel」という選択肢に着目します。次ページで紹介します。
Copyright © ITmedia, Inc. All Rights Reserved.
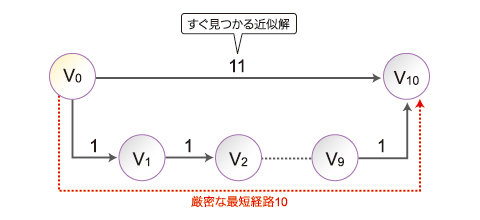 1回目のMapReduceで求まる近似解「11」と、10回目のMapReduceで求まる厳密解「10」のどちらの結果を求めますか?
1回目のMapReduceで求まる近似解「11」と、10回目のMapReduceで求まる厳密解「10」のどちらの結果を求めますか?


